【算法】图最短路径算法 —— Dijkstra
Dandelion 9/1/2022 algorithm
# 算法概述
- 问题定义:给定带权有向图 G 和源点 v,求 v 到 G 中其他顶点的最短路径
- 限制条件:图 G 中不存在负权值的边
- 核心思想
- 把图中顶点集合 V 分成两组,第一组为已求出最短路径的顶点集合(S),第二组为其余未确定最短路径的顶点集合(U)。
- 初始时,S 中只有一个源点 v,以后每求得一条最短路径,就将加入到集合 S 中,直到全部顶点都加入到 S 中,算法就结束了。
- 按最短路径长度的递增次序依次把第二组的顶点加入 S 中。在加入的过程中,总保持从源点 v 到 S 中各顶点的最短路径长度不大于从源点 v 到 U 中任何顶点的最短路径长度。
- 每个顶点对应一个距离,S 中的顶点的距离就是从 v 到此顶点的最短路径长度,U 中的顶点的距离是从 v 到此顶点只包括 S 中的顶点为中间顶点的当前最短路径长度。
- 贪心算法
- 在对问题求解时,总是做出在当前看来是最好的选择(局部最优解)。
- 不是对所有问题都能得到整体最优解,关键是贪心策略的选择,策略必须具备无后效性。
# 算法流程
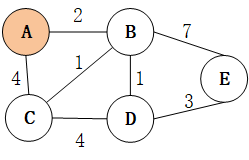
- 考虑:计算上图中的 A 点到其他节点的最短路径
- 初始化集合 S 和 U
- S = { AA(0) }
- U = { AB(2), AC(4), AD(∞), AE(∞) }
- 从 U 中找出路径最短的点,加入 S,并更新 U:
AB(2)- 如果 AB 的长度与 B 到 C/D/E 的距离之和小于 A 到 C/D/E 的距离,则更新集合 U。
- 第一次循环:
- S = { AA(0), AB(2) }
- U = { AC(3), AD(3), AE(9) },由于
4 > 1 + 2,AC 间的最短路径变为 3,以此类推。
- 循环执行上一个步骤,直至遍历结束(U 中无节点)。
- 第二次循环:
- S = { AA(0), AB(2), AC(3) }
- U = { AD(3), AE(9) }
- 第三次循环:
- S = { AA(0), AB(2), AC(3), AD(3) }
- U = { AE(6) }
- 第四次循环:
- S = { AA(0), AB(2), AC(3), AD(3), AE(6) }
- U = { }
- 第二次循环:
- 初始化集合 S 和 U
- 总结:按最短路径长度的递增次序依次把第二组的顶点加入 S 中
- A -> B 的最短路径:A -> B(2)
- A -> C 的最短路径:A -> B -> C(3)
- A -> D 的最短路径:A -> B -> D(3)
- A -> E 的最短路径:A -> B -> D -> E(6)
- 思考:为什么 Dijkstra 算法不适用于带负权的图?
- 当把一个点选入集合 S 时,就意味着已经找到了从 A 到这个点的最短路径,如果图中存在负权边,那么最短路径可能会发生变化。
- 对于带负权的图,可以使用弗洛伊德(Floyd)算法。
# 算法实现
function initMap(pathArr, target) {
let uMap = new Map();
for (const path of pathArr) {
if (path[0] === target) {
uMap.set(path[1], [target, path[2]]);
continue;
}
if (path[1] === target) {
uMap.set(path[0], [target, path[2]]);
continue;
}
if (path[0] !== target && path[1] !== target) {
if (!uMap.has(path[0])) {
uMap.set(path[0], [target, Infinity]);
}
if (!uMap.has(path[1])) {
uMap.set(path[1], [target, Infinity]);
}
}
}
return uMap;
}
function dijkstra(pathArr, target) {
// 初始化 sMap/uMap
let sMap = new Map();
sMap.set(target, [target, 0]);
let uMap = initMap(pathArr, target);
// 循环遍历 uMap,找到 uMap 中距离目标点最近的点,加入 sMap,并更新 uMap,直至 uMap 为空
while (uMap.size !== 0) {
// 找到距离目标点最近的点
let temp = Array.from(uMap).reduce((res, v) => {
return res > v[1][1] ? v[0] : res;
}, Infinity);
// 加入 sMap
sMap.set(temp, uMap.get(temp));
uMap.delete(temp);
// 更新 uMap
let tempMap = initMap(
pathArr.filter((v) => v[0] !== target && v[1] !== target),
temp
);
for (const u of uMap.keys()) {
let dist = tempMap.get(u)[1] + sMap.get(temp)[1];
if (uMap.get(u)[1] > dist) {
uMap.set(u, [target, dist]);
}
}
}
return Array.from(sMap).map((v) => [target, v[0], v[1][1]]);
}
let pathArr = [
['A', 'B', 2],
['A', 'C', 4],
['B', 'C', 1],
['B', 'D', 1],
['B', 'E', 7],
['C', 'D', 4],
['D', 'E', 3],
];
console.log(dijkstra(pathArr, 'A'));
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
let INF = Number.MAX_SAFE_INTEGER;
function minDistance(dist, visited) {
let min = INF;
let minIndex = -1;
for (let i = 0; i < dist.length; i++) {
if (!visited[i] && dist[i] < min) {
minIndex = i;
min = dist[i];
}
}
return minIndex;
}
function dijkstra(src) {
let dist = [];
let visited = [];
let length = graph.length;
for (let i = 0; i < length; i++) {
dist[i] = INF;
visited[i] = false;
}
dist[src] = 0;
for (let j = 0; j < length - 1; j++) {
let u = minDistance(dist, visited);
visited[u] = true;
for (let v = 0; v < length; v++) {
if (
!visited[v] &&
dist[u] !== INF &&
graph[u][v] !== 0 &&
dist[u] + graph[u][v] < dist[v]
) {
dist[v] = dist[u] + graph[u][v];
}
}
}
return dist;
}
let n = 6;
let graph = Array.from({ length: n }).map((v) =>
Array.from({ length: n }).fill(0)
);
let pathArr = [
[1, 3, 4],
[3, 2, 5],
[1, 4, 6],
[4, 5, 2],
[4, 6, 3],
[2, 1, 3],
[3, 1, 4],
[4, 1, 3],
[5, 1, 5],
[6, 1, 2],
];
let roadArr = [],
res = [];
for (const [a, b, c] of pathArr) {
roadArr.push([a - 1, b - 1]);
graph[a - 1][b - 1] = c;
}
let operArr = [
[2, 1, 5],
[2, 6, 5],
[1, 4, 3],
[2, 1, 6],
[2, 6, 5],
[2, 3, 5],
];
for (const [t, u, v] of operArr) {
if (t === 1) {
let [a, b] = roadArr[+u - 1];
graph[a][b] = +v;
} else {
const min = dijkstra(+u - 1);
res.push(min[+v - 1]);
}
}
console.log(res);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
